Probably, the most noxious one is the one that equates a high B.C. to a "good" projectile and a low B.C. to a "bad" projectile.
B.C. is NOT a measure of the "design qualities" of a projectile.
So. . . . ¿What is BC?
First and foremost, BC is a SCALE FACTOR.
To explain this we need to go back almost two hundred years, to the heroic days when small, field worthy artillery pieces were truly coming into their own. When smokeless powder first became a commercial and military reality, and when the value of a soldier's life was less than the value of the musket he carried.
So, imagine yourself living from the 1840's to the late 1880's:
The US has just doubled its territory by waging war on México.
Crimea has just been lost by the Russians to a Western European bloc
Germany has just annexed all the Alsace Lorraine
The French have just invented the "75" and Captain Dreyfus is spending some time in "Devil's Island" because it is easier for the "Establishment" to send an innocent person to his death in a tropical island than to accept that the ring of spies is so well entrenched in the government circles as to make it a "Reason of Sate".
Russia is trying to assert its role in the "modern world" and the Czar decides to support the Army because supporting the Navy, with no warm water sea port is senseless. There is a peculiar alliance being established between France (the 3rd Republic) and Russia (an Imperial Autocratic State).
Out of England (THE Maritime Power of its day), comes a young chap by the name Francis Bashforth; developing on the (by then 200 years old) ideas by Benjamin Robins, he creates in the late 1860's an electromechanical chronograph that is capable of measuring velocities of projectiles to much greater precision than the ballistic pendula of the day. Consider that to measure ACCURATELY, a ballistic pendulum has to have a mass at least 200 times greater than the projectile it tries to measure. Now consider the size of ballistic pendula for artillery ogives.
Bashforth measures and creates tables for all his measurements, and then comes up with a flash of brilliance:
¿What if ALL the effort was devoted to a "standard" projectile, could he then prove that all other projectiles would have a SIMILAR behaviour?
Similarity, in the mathematical context, is the capacity to change one thing into another using a scale factor.
And so, he proposes the Ballistic Coefficient; a SCALE factor that can tell technicians how a given projectile will behave BASED on a LOT of firings of a STANDARD projectile.
Being a good Yorkshireman, and VERY British, Bashforth uses a Standard Projectile (S.P.) of 1.00" Caliber, with a 1.5" tangent Ogive, weighing (¿What else?) 1 lb. And this becomes the B.C. = 1.00
Now, let's come to the present and analyze this a little: ¿What on earth can be MORE DIS-SIMILAR than a flat base, 1.5 calibers tangent ogive, parallel sides projectile, weighing all of 7,000 grains in 1.00" Cal. AND an 8.44 grains, diabolo shaped (waisted) pellet with an ogive barely 1.25 calibers in cal. 0.177"?
Caliber of the S.P. is more than 5½ times the caliber of the projectile we are interested in.
Mass of S.P. is more than 800 (eight HUNDRED) times the mass of the projectile of interest.
There is NOTHING of the S.P. that barely resembles our pellets. How can we HOPE to use a simple SCALE factor?
Well, we can't.
And neither can do many others interested in the exterior ballistics.
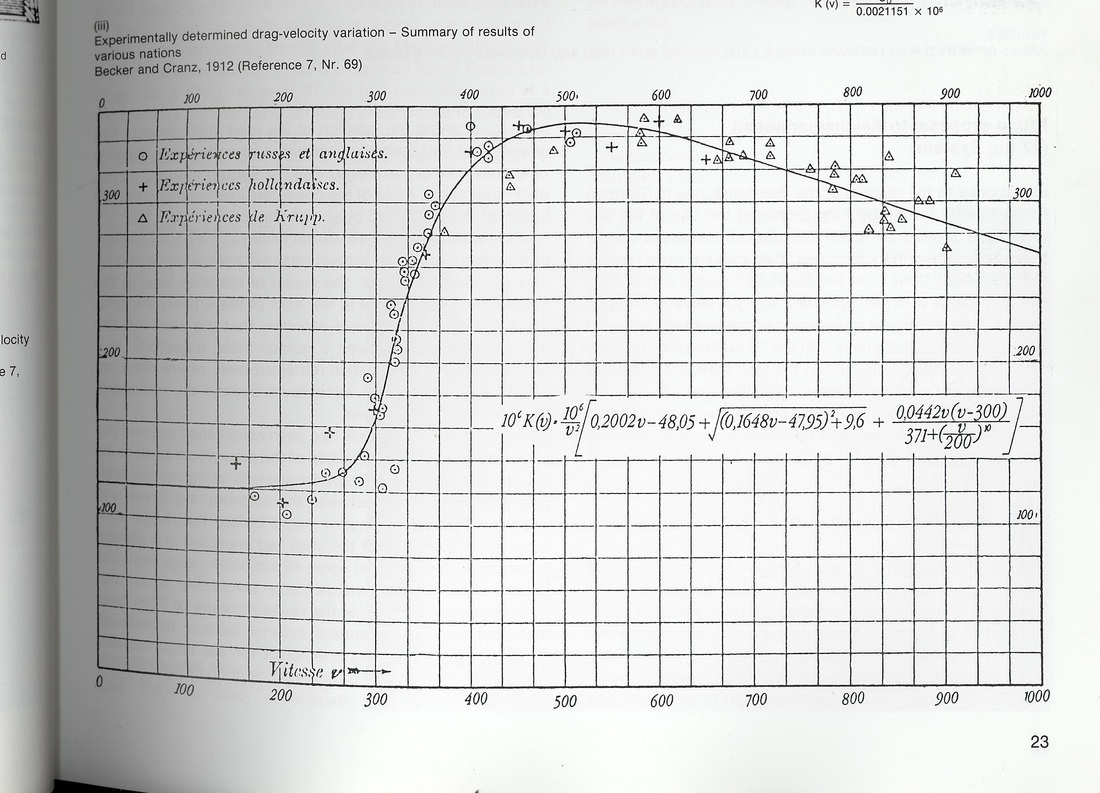
Going back to the late 18th Century, the Russian Mayevski, then the Italian Siacci and then the American Ingalls, conducted a LARGE number of tests. At the same time, Krupp was conducting their own experiments and by 1875-1890 all nations had a pretty well informed knowledge of what exterior ballistics truly meant, as far as field artillery pieces were concerned. Just in time for the Balkan Wars, and then World War I.
Now, please consider: IF drag changes like this for every speed along the pellet's projectile, then the B.C. that is trying to scale a whole trajectory is much more dependent on how closely the projectile of interest is to the S.P.
It was the Russian, the Italian and the American, the ones that first proposed a DIFFERENT way to look at things: ¿Why not develop a mathematical model that, taking into account the physical characteristics of the projectiles will give us firing solutions?
Ah! that sounded GREAT!, let's call it Drag Function and then we can PREDICT what things will behave like as long as we know how those physical characteristics relate to the external ballistics.
At first it seemed that a "form factor" could be established that related the B.C. to the sectional density (the weight of the projectile -in lbs.- divided by the square of the caliber), BUT then the form factor became something to be qualitatively assigned. Tables were prepared where by graphical observations, shooters could ascertain which form factor they could use for their bullets.
REAL problem is that reality is a little too rich in details and too complicated to actually be able to do this with any really good precision. Few functions are linear, and since the old days, the exterior ballistics solutions have been, in reality, approximations by velocity regions. One set of equations, constants and coefficients apply from 0 to about 850 fps, another from 850 to about 1,100, another from 1,100 to about 1,400, then another between 1,400 and 2,200, and another between 2,200 and 5,000 fps.
Even at present, military applications use one Drag Function and commercial applications use another.
In the market there are several programs and types of software that use the drag coefficients. BUT they all have the same caveat: Use only by sections and make sure that YOUR case is not close to the boundaries of the sections. A few really good and conscientious manufacturers publish the B.C.'s for their bullets by MV regions.
In more recent times, with the advent of cheap and relatively reliable and precise chronographs, it has become easy to determine the "deceleration" (loss of velocity) of ANY projectile, and there have been some rather interesting approaches to solving the firing solutions.
Among the more imaginative is Pejsa's "Velocity Retention Factor", and similar approaches whereupon some of the modern airgun pellet ballistics programs work.
The BEST mathematical model taken from the dimensions of the newly produced pellet will NOT be true once you fire that pellet through ANY barrel.
Modern pellets and modern barrels do this less dramatically than those made only a few decades ago. Compare the above picture to this one:
So, there is NO way to use a "table" B.C. for your pellet calculations, if you want them to be precise.
One of the peculiar differences between airgun shooters and powder burners is that, for them, some differences are "small" or "inconsequential". For airgunners where the targets are measured in fractions of an inch, there is no really inconsequential difference.
Especially for FT shooters.
A 40 Troyers target (a measure of relative difficulty) is a ½" target at 20 yards. The pellet occupies 0.177" of that, so the real wiggle room is about 0.32" If you consider that the pellet needs to be LESS than one caliber off to any side from center, you realize how accurate FT shooters and gear have to be.
And that is not the hardest target in an FT course, Match Directors can place these ½" targets all the way out to 30 yards! for a 60 Troyer shot.
It seems to be one of those things that you are bad with it, and even worse without it.
For years I used Pejsa's approach and tried to calculate and keep good records of Velocity Retention Coefficients for all pellets in all my rifles. And then we went to Norway to shoot at the FT World's Matches and I got faced with wind drift.
This is the OTHER side of B.C.: ONCE YOU HAVE A TRUE B.C. then wind DOES become a scientific calculation.
Not only that, Wind drift is proportional to normal velocity (velocity vector measured perpendicular to the trajectory plane). So, if you could have the B.C. for YOUR pellet, shot from YOUR rifle, at the place you ARE shooting, then wind drift is really more a matter of learning how to "guesstimate" this normal wind velocity.
BUT. . . chicken and egg situation! How can I find the B.C. of my pellets shot at places as dis-similar as Norway (coastal location), Germany (mountain location), Texas (lowland, dry location), or Baton Rouge (humid, coastal location). ¿Should I take my two, matched, Chronos and do all my testing all over again?
¿At EVERY venue?
Well, enter a different point of view and a recently modern mathematical approach called "Fuzzy Logic", where one quantity can have not only A value, but a RANGE of values. Then you go on the next "test case" and check that range of values against the new one, and by discarding those values that are OUTSIDE BOTH ranges, you have a narrower range. Then you take a THIRD test case and come up with a different range of values, when you compare all three and come up with the value that meets all three test cases, then you have your solution.
This is how P-P Calc works.
And that is why I came back to the B.C. method. By using a zero range and THREE more ranges and POI's, the software calculates the B.C. by sections of the pellet path, it will give you a weighted average and use that for the calculations, but more importantly, it will calculate the wind drift.
While discussing the error in B.C.'s vs. the Wind Normal Velocity reading error with a very good shooter, Scott Hull, he came up with this example:
As much as we dislike the idea, we cannot fault our pellets for having such a low B.C. (just to illustrate, some modern 0.50" cal bullets have B.C.'s GREATER than 1.00)
The low B.C. is what makes the use of our pellet rifles relatively safe in urban environments and at close distances.
The low B.C. of our pellets is what gives us the same challenge shooting out to 55 yards as the H.P shooters get shooting at 600 yards.
The low B.C. of our pellets is what makes our sport unique.
In conclusion:
Pellet shooters CAN use the B.C. concept, but they need to be careful to apply it by sections.
"Fiddling" with the B.C. is not too smart unless you REALLY know your rifle/pellet combination well. You may arrive at a scale factor (the B.C.) that has nothing to do with reality.
P-P Calc will allow you to MEASURE the B.C. from YOUR rifle/pellet combination at EVERY venue. You can then store that venue for future reference.
Hope this has been informative and I hope to see you at some FT Match soon!
HM




 RSS Feed
RSS Feed