Anyway, among the things that military science developed in Switzerland is the milliradian. The root of the "Mil" section in "mil-dots". It was invented by Charles Marc Dapples, around the late 1800's, and by 1914, more than a few countries had already adopted it. France being the first one, as it needed a better sighting and ranging method for their "75" the first truly worthwhile field artillery piece.
Later, in the 1950's NATO standardized to metric units and the milliradian became the standard unit of measure for angle.
So, exactly WHAT is a milliradian? Well, a milliradian is the 1/1000th part of a radian, and before you say: "Dooohhh", let me explain that a radian (rad.) is the angle subtended when the LENGTH along the circumference is the same as the radius of said circumference. This curious definition defines an ANGLE using a CURVED line and a straight line. ¿WHY?, well, Monsieur Dapples was a mathematician and an engineer, and he liked absolute precision in concepts but practical ways for applications; because the relation between a circumference and its diameter is the number "Pi" (also expressed as the greek letter π), that is an endless number, he wanted to be precise but he did not want to write the digits of one number for the rest of his life. So, by using "π" , he was at the same time, scientific and engineering. He was expressing the EXACT relation, but for engineering calculations (slide rules in those days, no calculators and, even less, computers), he could approximate very well (all engineering slide rules have π marked in the scale). So he "discovered" that under the definition of his "radian" as an angle unit, the circumference had 2π radians (remember the circumference of a circle is π x diameter, and that the diameter is twice the radius, so the whole circumference measures 2πr), or ≈ 2x3.141592652xr
From the above, you could say now that if 360º= 2π, then 1radian≈57.2958º, or that 1º≈17.4533 mrads
Up to that point, the UTILITY of the mrad lies only in the manufacture of clocks, where gears and gears and more gears are used to divide the time into the smallest pulsations possible, thereby enabling the clock or watch to be more and more precise; BUT, ¿HOW did the mrad jumped to artillery and then to riflemen usage?
Well, we need to understand at least ONE concept of trigonometry: the sine.
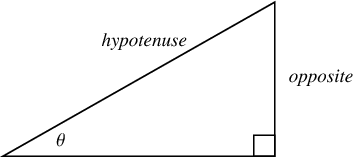
Before you get scared, look at this picture:
One of those relations is called "sine". And it is defined as the length of the opposite divided by the length of the hypotenuse:
sine(Θ)= opposite/hypotenuse
Now, imagine that the opposite side was a section of a circumference whose center is the corner where the Θ letter is located, it would not be straight, but it would have a length. If that opposite side was the SAME length as the "nameless" side in the diagram (usually called the adjacent, but let's leave it as "nameless" for fun), then the LENGTH of the opposite would be the SAME LENGTH as the radius that generates the opposite (the "nameless" length), and then Θ = 1 rad.
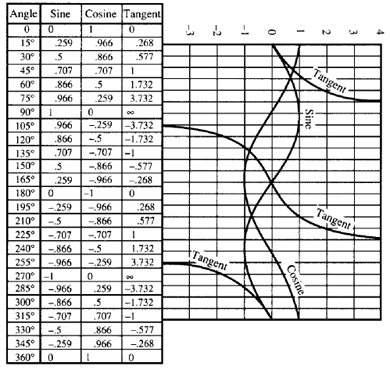
Now, here comes the magic, and because I do not want to bore you with more maths, let's look at a table:
sine(90º)=1.000
sine (75º)=0.966
sine (60º)=0.866
sine (45º)=0.707
sine (30º)=0.500
sine (15º)= 0.259
sine (0º)= 0.000
BUT (always a big BUT somewhere!, LOL!), when expressed in radians:
sine (90º≈1.57rads)=1.000 (difference between rads and value of sine = .57)
sine (75º≈1.31rads)=0.966 (difference = 0.34)
sine (60º≈1.05rads)=0.866 (difference = 0.18)
sine (45º≈0.79rads)=0.707 (difference = 0.083)
sine (30º≈0.524rads)=0.500 (difference = 0.024)
sine (15º≈0.262rads)=0.259 (difference = 0.003)
sine (0º=0rads)=0, difference ZERO.
We therefore KNOW that for SMALL angles the angle in rads and the sine of the angle have almost the same value because we have analyzed that the differences become smaller and smaller.
IF the angle in rads (or millirads, to use the "zone" we are talking about) has the same value as the sine of that angle, then the original definition of sine above:
sine(Θ)= opposite/hypotenuse
Can also be expressed in more useful terms: Hypotenuse = Opposite/sine(Θ)=1000 x Opposite/mrads
If we translate trigonometric terms to shooting terms then:
Range = 1000 x (known dimension of target / mrads) and the mrads is what we measure with the marks of our scopes' reticules (when the reticule is either First Focal Plane, or set at its "true" magnification).
For example: If I know that my target is 1 yard high (a small Roebuck) and the whole animal can be fitted between the centers of two consecutive dots, or between two consecutive unit hashmarks, then I know that buck is 1,000 yards away. If said buck occupied TWO dots, then it is 500 yards away, if it occupied 4 dots, then it is 250 yards away (now it is a doable shot at such small quarry).
Of course, if I know that my zero is at 250 yards, then I can take the shot with "no hold" (either over, under, left or right), but if I know where my trajectory is at all distances, then I can hold to the EXACT point where I KNOW I will hit the target. I can ALSO allow for wind.
This is the "principle" of bracketing, this is WHY it works. There are plenty of writeups in the web about the usage of mil-dots in different units, different configurations (Army vs. Navy), different reticules, formulae and even places where you can buy the modern version of a specific slide rule, called the Mil-Dot Master that makes Imperial Unit users get the numbers right.
I will not go there. For me it is dead easy because I am metric and in metric units if you express the height or width of an object in milimeters, and use true dots or hashes, you get directly the range in meters.
Because the relation between range and target size starts from a basic relation of 1:1,000, you need to find a place where you can set a construction ruler (one of those squares/rulers that are used to mark and and cut gypsum board) at 83 feet and 4 inches (83' 4"). ¿Why that specific distance? simple! there are 1,000 " in 83' 4"; and the rulers and squares we are talking about come marked in inches and fractions thereof.
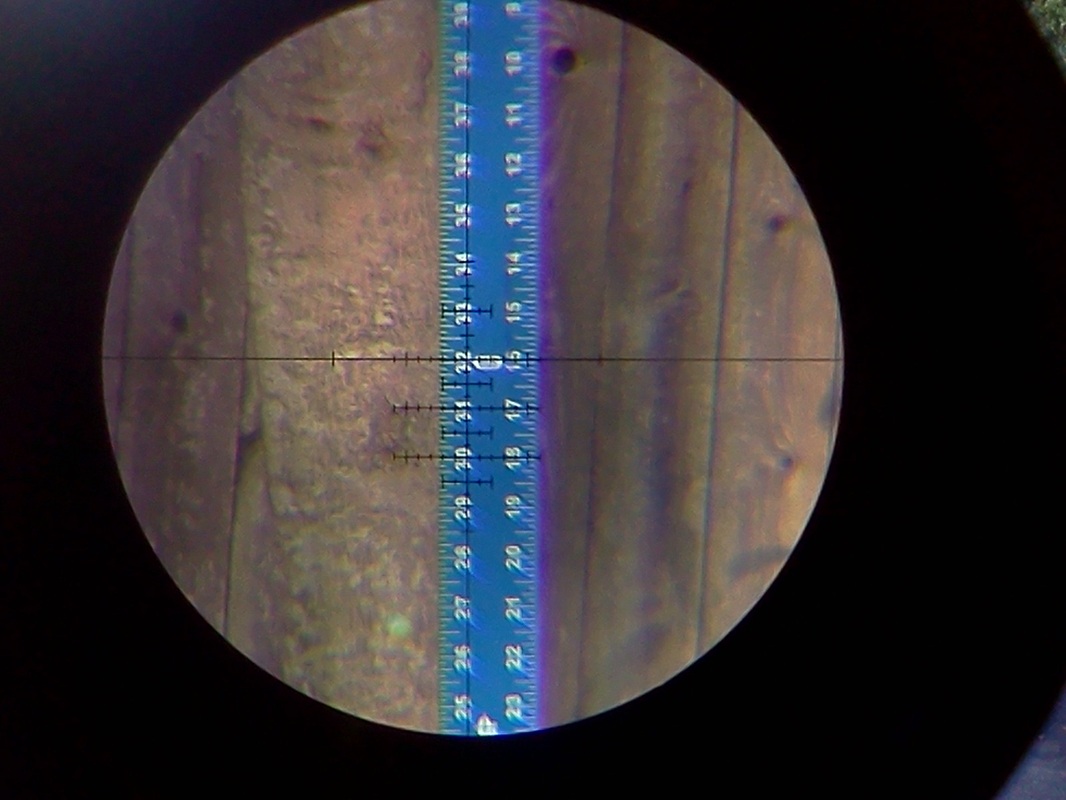
So you need to setup something like this:
And then you fiddle with the mag ring till the most extreme marks in your reticle align with the inch marks in the ruler. Sometimes it takes more than a little fiddling, but patience here will yield huge rewards later, as you will be CONFIDENT of what you are measuring with.
Do note that in this scope, the sizes of the marks are VERY consistent, even across half of the field of view of the riflescope.
This is not common in "economy" scopes and it is one of the reasons why we like the AEON brand of riflescopes.
Also note that for every full unit mark, the AEON scopes have 4 intermediate marks, thereby allowing us to measure not only in mrads, but in ¼ mrads and estimate up to 1/8 mrads.
The greater resolution in the measurement AND in the hold-off are very important in Field Target, especially when shooting in the southern clubs of the US of A that love tiny Kill Zones.
In case you have one of the economy scopes that are "true" at 10X, but you have, at least, up to 12X magnification in your zoom ring, you still have one more thing you can do:
First ensure that your reticle is TRUE at 10X using the above procedure.
Then move the ruler to the 100' line and set your magnification at 12X, you SHOULD see that the dots in the reticle and the inches in the ruler coincide. This is because at 12X, the reticule is no longer mrad, but it does measure IPHF (Inch Per Hundred Feet) angles, and the approximation of sine to length still works. So you CAN use your 12x/true at 10X scope to do the ranging and the hold, BUT you need to ensure that the field of vision is FLAT (the last distance between dots measures the same as the first one), and you would be wise then to use your range card in feet, not yards.
Hope this helps!
HM



 RSS Feed
RSS Feed