Group statistics: What can target groups tell us about the accuracy of an air rifle?
Before we discuss group size at a target, let’s first look at an illustrative example of statistics at work.
Let’s say we wanted to predict the weight of the largest haddock that will be caught by a fishing boat from Maine in the next year. We can do this by looking at the catch of haddock from that fishing boat on just one day!
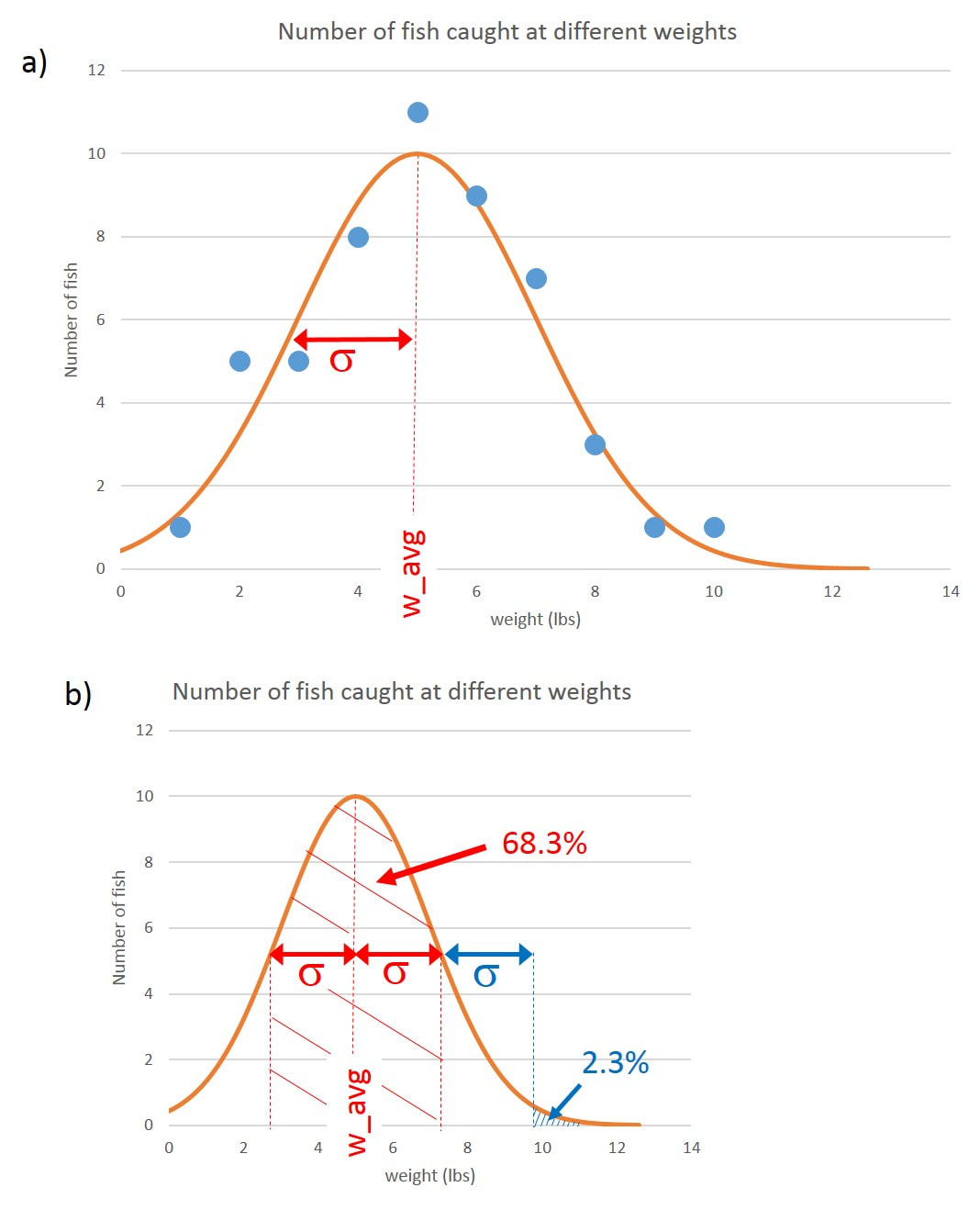
Figure 3.1a) shows the number of haddock as a function of their weight (blue circles) that were caught on one day. In this case, one fish weighed 1 lb, five fish weighed 2 lbs, another five fish weighed 3 lbs, and so on. This distribution looks like the good old bell curve and can be fitted by a Gaussian function (orange curve in Fig. 3.1a); don’t worry about what the equation for a Gaussian looks like!
This is also called a normal distribution since it is symmetric, with the average (w_avg), peak, and median (divides the top and bottom half of the distribution) values all same (around 5 lbs). The bell curve will also have some width (σ), which tells us how much variation there is in the weights. You can also think of the bell curve as representing the probability that a fish of a certain weight will be caught. The probability of catching a 5-lb fish is about twice that of catching an 8-lb fish. The further the weight of the fish is from the average 5-lb value, the less likely that fish will be caught. It turns out, that a Gaussian distribution has well-defined probabilities that depend on how far a particular sample (in this case, a single fish) is from the average value. For example, 68.83% of the fish caught will have weights within ±σ of the average value. This is shown by the red hashed region between 3 and 7 lbs in Fig. 3.1b). Only 2.3% of the fish caught will have weights that are 2σ or more above the average weight. This is represented by the blue hatched region above 10 lbs in Fig. 3.1b). What are the chances of catching a fish that is over 12 lbs? 12 lbs is about 3σ above the average weight and about 2.4 times the average weight of 5 lbs. Please note that 3σ away from the average is not the same as three times the average! It just means that we take the average value and add 3σ to it. For a Gaussian distribution, the number of samples that are 3σ or higher than the average is 0.14%. That translates into about one out of every 700 fish caught being over 12 lbs. So if the captain is hoping to catch a fish greater than 12 lbs, he needs to catch around 700 fish to have a good chance of one of them being that heavy. Of course, the first fish the boat catches may be a 12-pounder, but that is very unlikely. Also, we had to assume that the day’s sample is representative of the larger haddock population in the area and that nothing horrible (like an algae bloom) happens to disrupt that population during the year. Although one could in principle keep track of all the haddock in the ocean and therefore predict what we’ll catch and where, this would be absurdly impractical, so we need to use statistics to make predictions. Opinion polls work the same way, where one uses smaller sample size to figure out what a much larger group of people is thinking.
Also, how many shots should we put in each group?
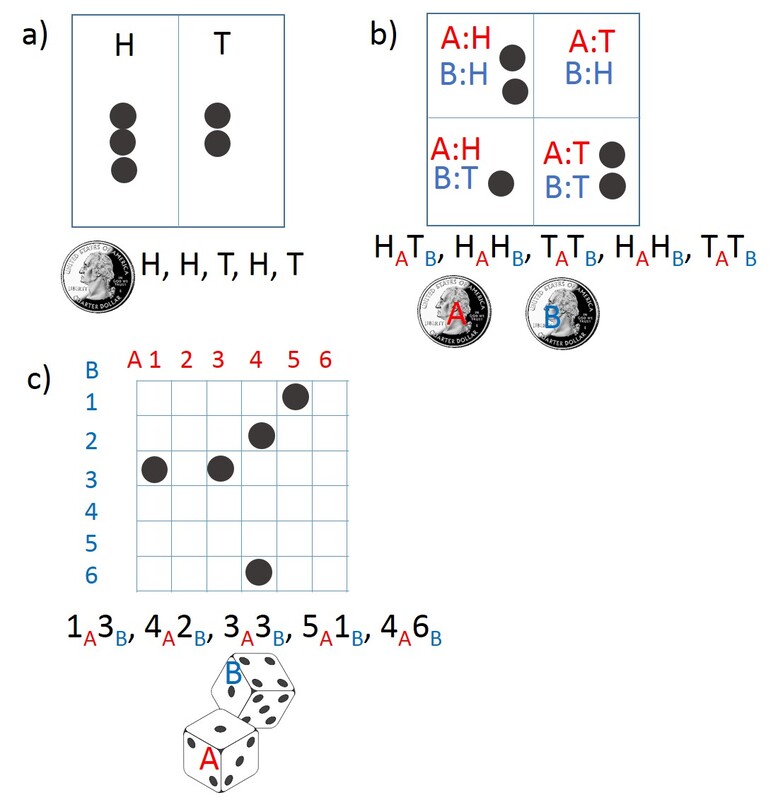
Before we start talking about pellet groups at a target, it helps to introduce one of the most fundamental ideas in statistics, the random walk. My favorite way to discuss the random walk is with a simple story. Imagine a drunken sailor who starts walking along a line. Sorry all you sailors out there, but the drunken sailor walk is a pretty standard concept in statistics! It also fits with the fishing theme that we explored at the beginning of this chapter. The sailor, let’s say Captain Haddock for you Tintin fans, has a 50% chance of stepping forward and a 50% chance of stepping backward after each step. Where will the sailor wind up after 10 steps? To answer that question we need to look at statistics. If we do this experiment over and over again, we’ll find that we get a distribution of final positions of the sailor after 10 steps. Most of the time, the sailor will be back close to his starting position after taking nearly the same number of steps forward and backward. There are lots of ways to get 5 steps forward (F) and 5 steps backward (B). For example, he could do 5 steps forward followed by 5 steps backward (FFFFBBBBB). He could alternate going forward and backward (FBFBFBFBFB). You can see that there’s lots of ways to arrange 5 Fs and 5 Bs to write the sailors stepping history. In fact there’s 252 ways to arrange 5 Fs and 5 Bs in a string of 10 steps. What the farthest the sailor could be from the starting point after 10 steps? That is simply 10 steps forward (or 10 steps backward). There’s no way he could wind up 11 steps from the starting position since he only took 10 steps. So how likely is it that the sailor winds up 10 steps in front of the starting position? Well, there is only one way to do this, with the sailor taking all 10 steps forward (FFFFFFFFF). One of the most important principles in statistics is that the more ways a certain result can be achieved, the more likely it is to happen. It turns out the probability that the sailor winds up 10 steps in front of the starting point after taking 10 steps is 1/1024=0.001, where 1 represents the number of ways the sailor can take all 10 steps forward and 1024 is just the number of all possible outcomes. There are 2*2*2*2*2*2*2*2*2*2=2 to the tenth power=2^10=1024 possible outcomes since for every step there are two possibilities and the possibilities multiply to get the total number of possibilities. We use the caret symbol ^ to indicate an exponent or “to the power of.” On the other hand, the probability that the sailor winds up back at the starting point is 252/1024=0.246, where 252 is the previously calculated number of ways to combine 5 Fs with 5 Bs and the 1024 is the total number of possible outcomes. So the sailor is 252 times more likely to wind up at the starting position than 10 steps in front of the starting position!
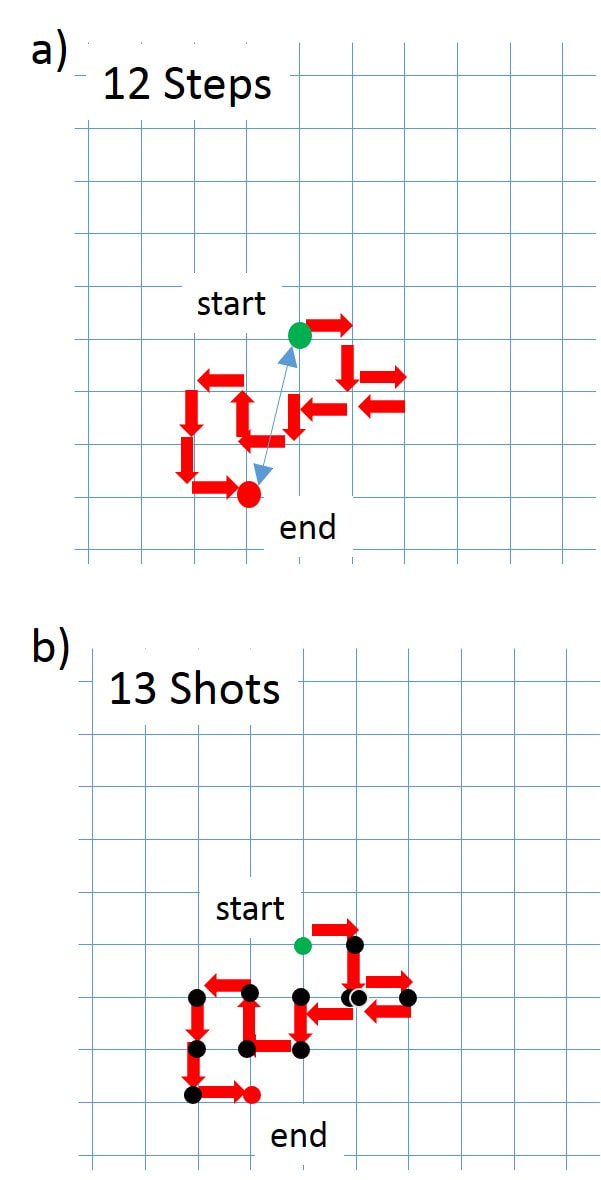
We can extend this random walk to two dimensions by allowing the sailor to step left or right as well as forward or backward. So for each step, there’s a 25% chance the sailor will go forward, a 25% chance he will go right, a 25% chance the he will go backward and a 25% chance he will step to the left. This is shown for 12 steps in Fig. 3.2a). This type of thought experiment can also be applied to shooting pellets at a target. I’ve coined this the “drunken marksman” problem where there’s a 25% chance that a shot will be one unit up, right, down, or left from the previous shot. As you can see in Fig. 3.2b) this is starting to look like a group of shots at a target!
https://www.snipershide.com/precision-rifle/22lr-lot-testing-at-lapuas-indoor-100m-test-facility-what-should-you-expect-in-gains/
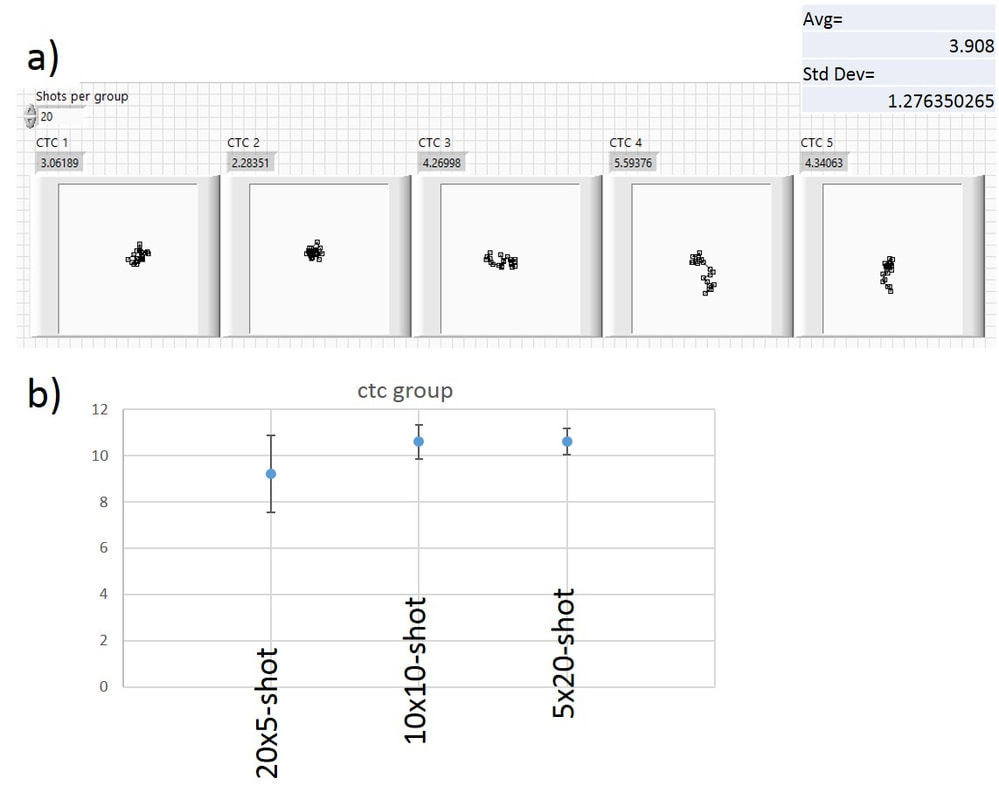
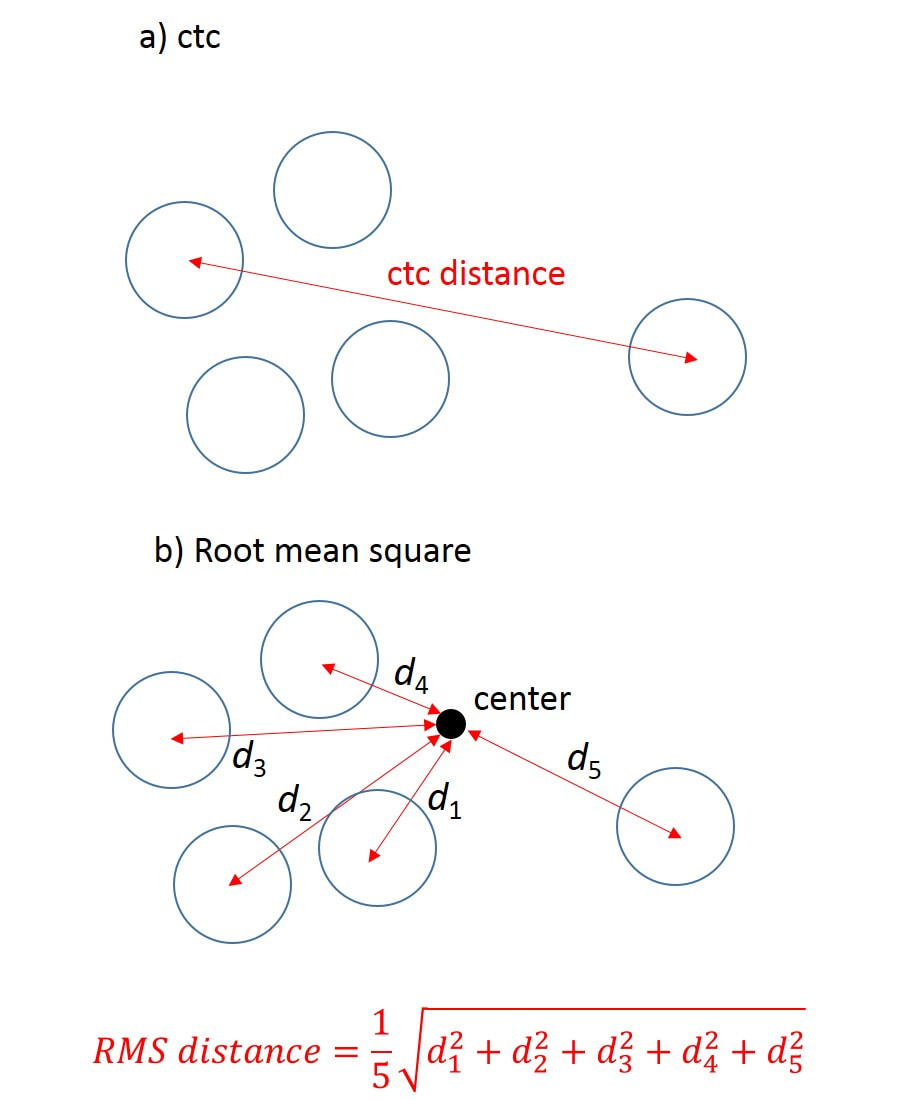
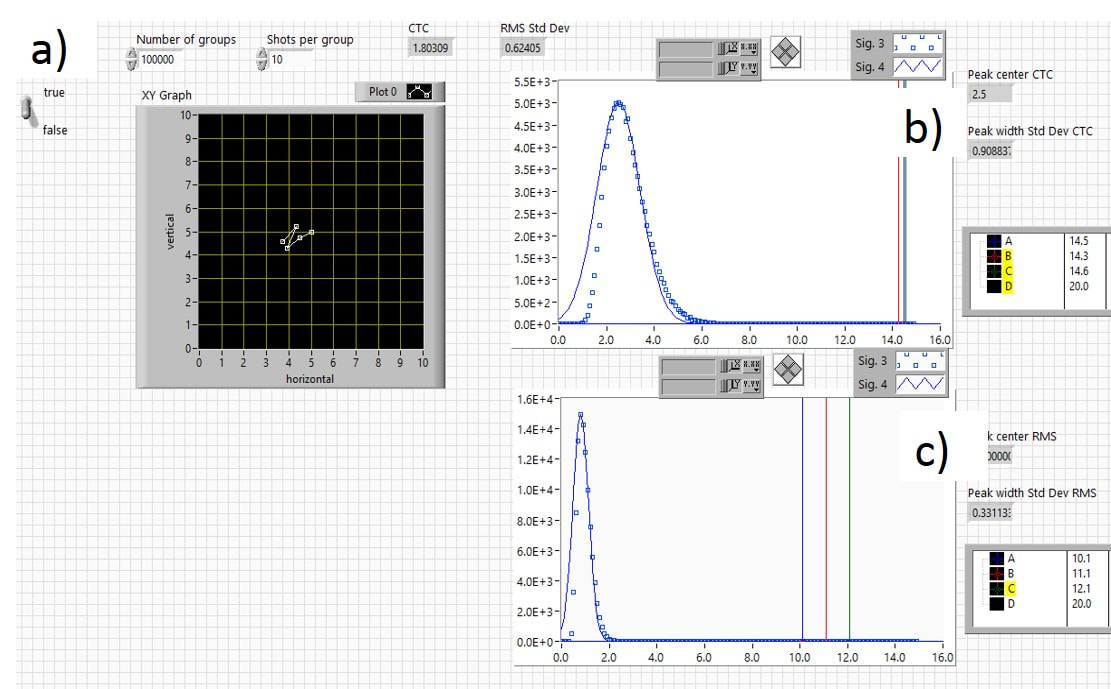
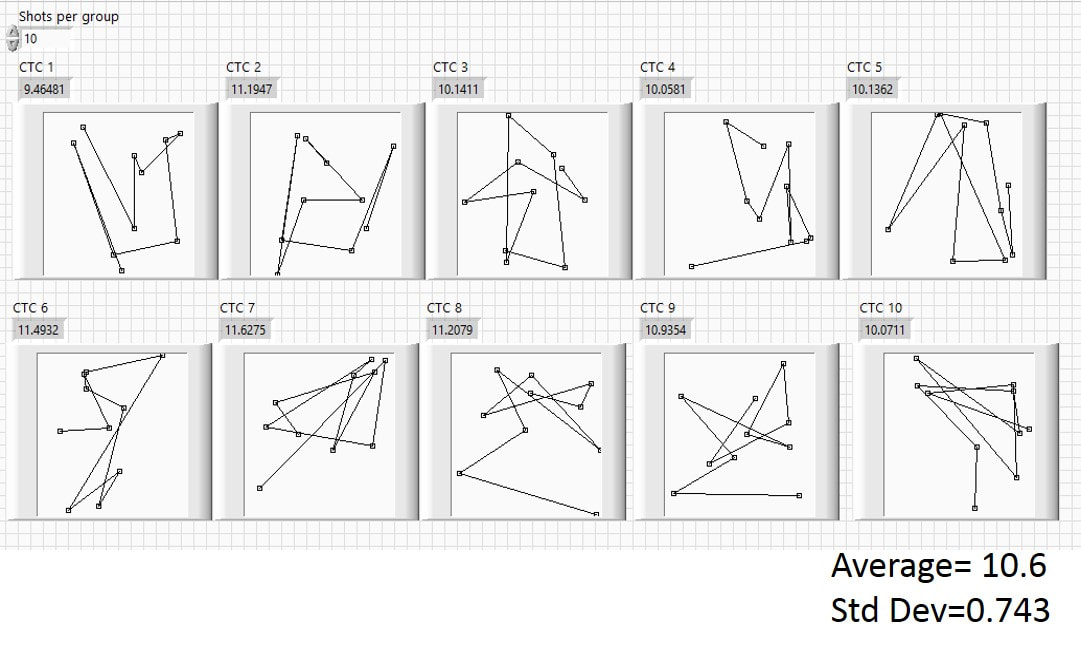
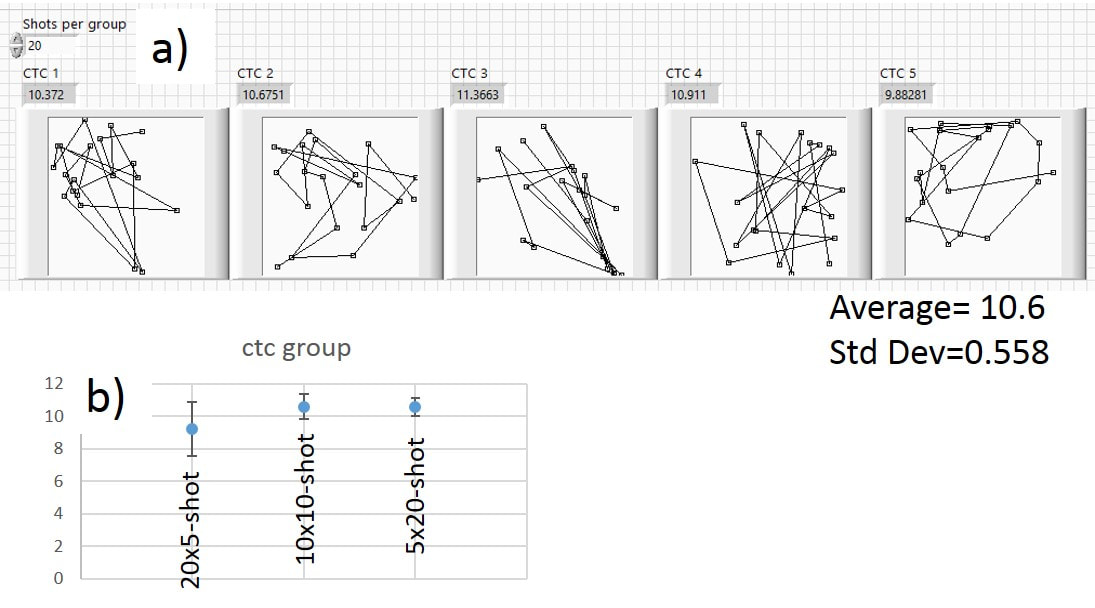
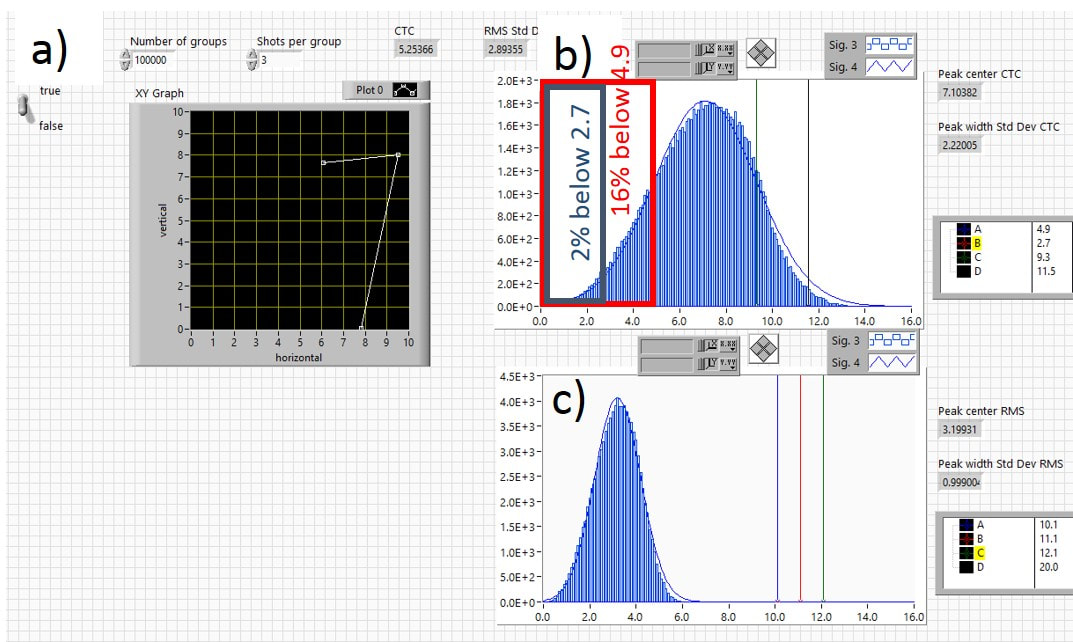
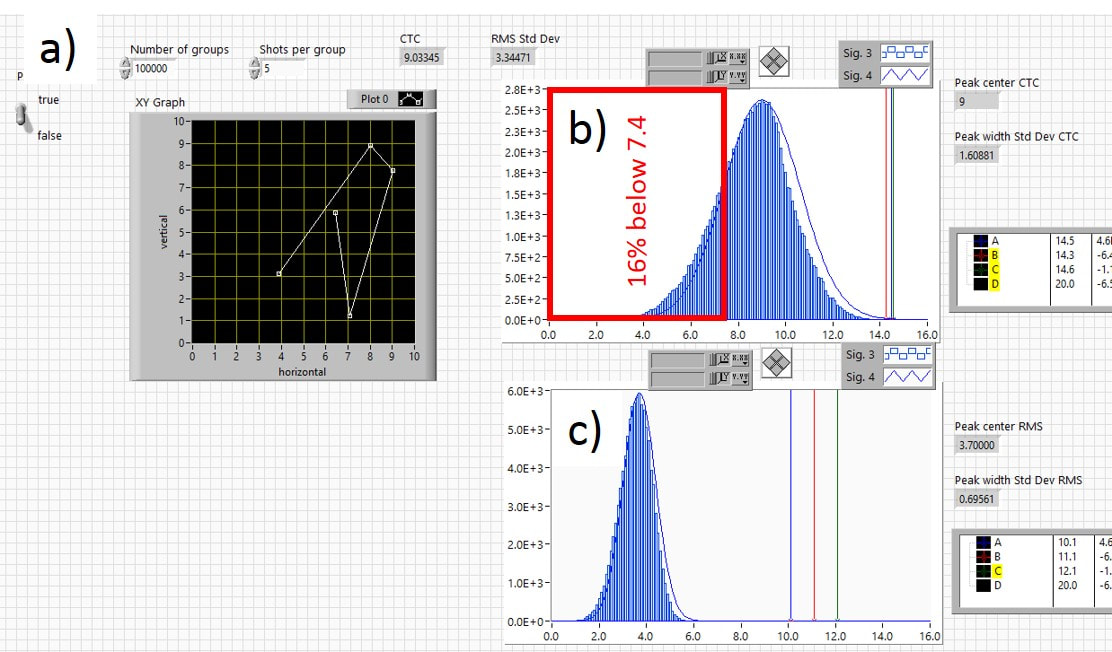
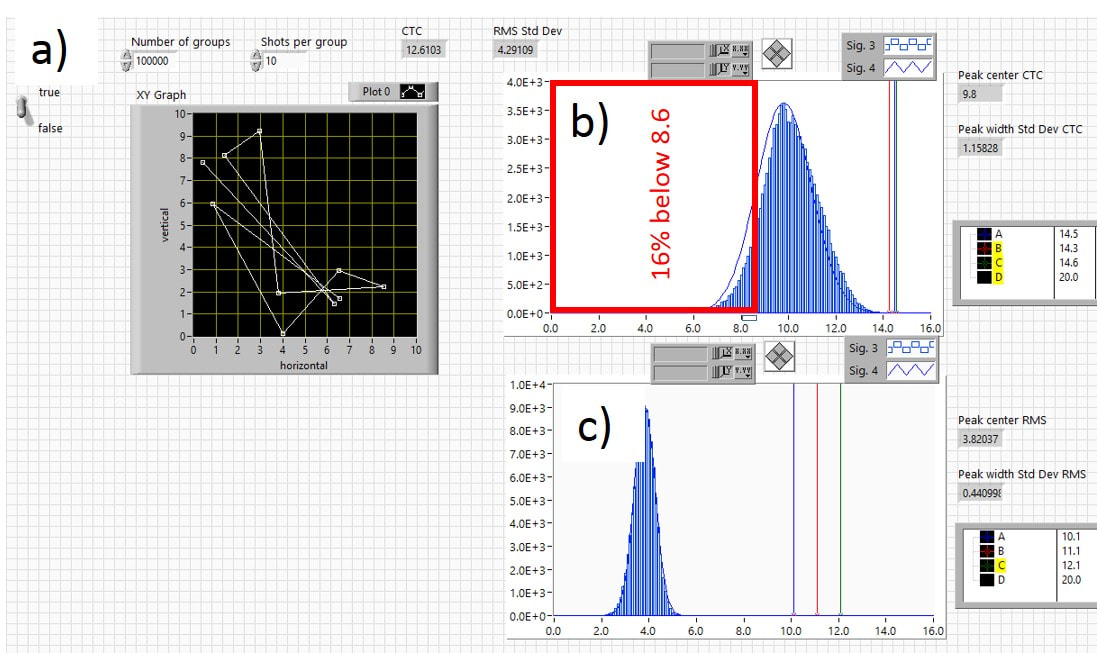
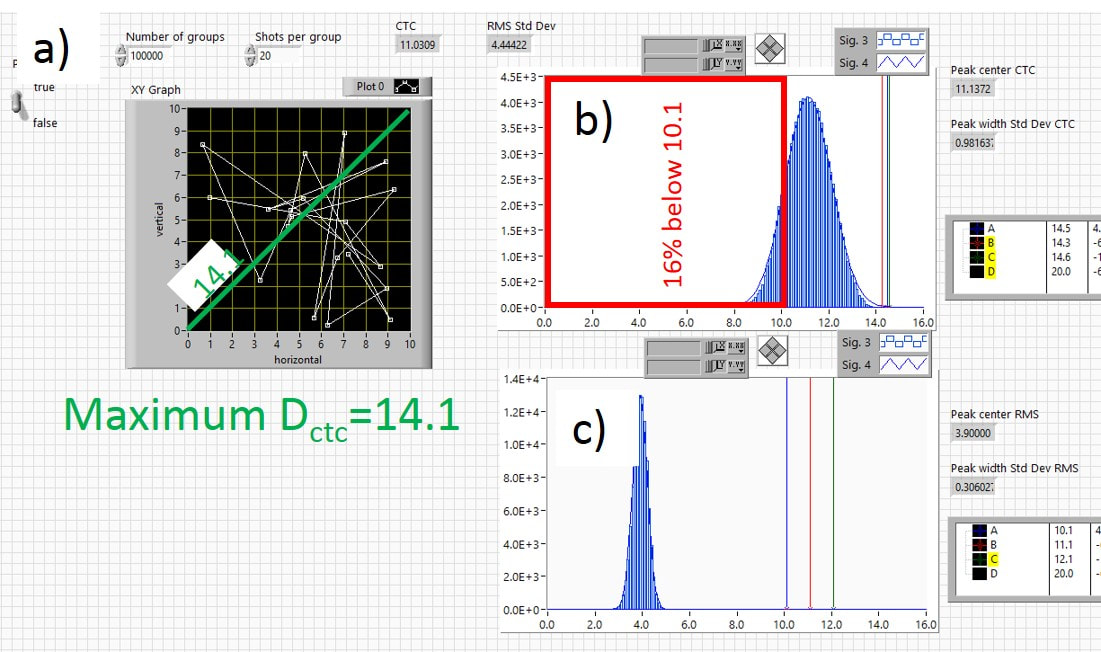
Figures 3.16 b) and c) show the distributions of the ctc and RMS distances, respectively, for 20-shot groups. Now the distributions are fitted really well by Gaussian functions! The 20-shot distributions have slightly larger averages and are slightly narrower than the 10-shot distributions. Clearly, adding more shots after 10 is not making much of a difference!
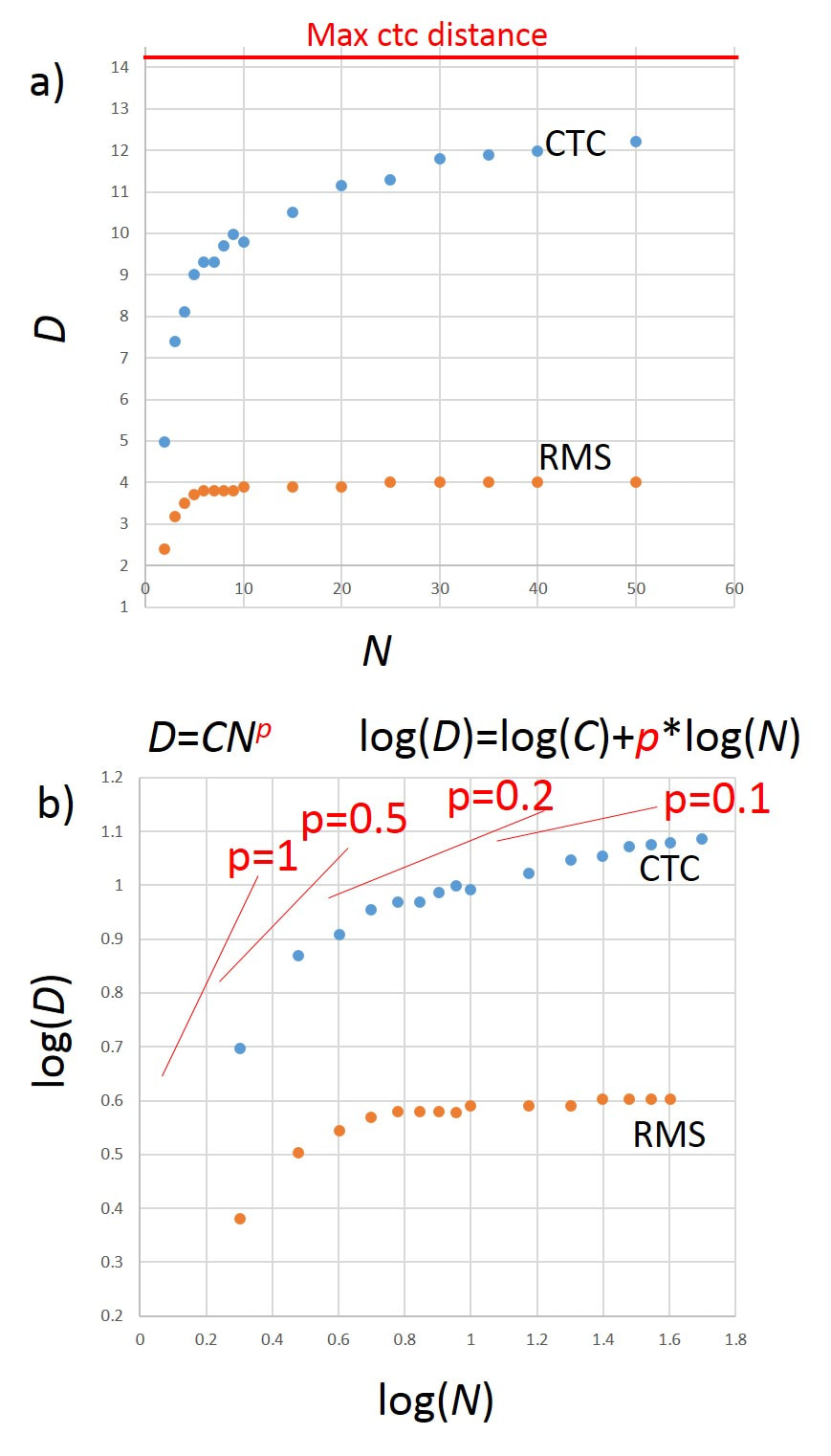
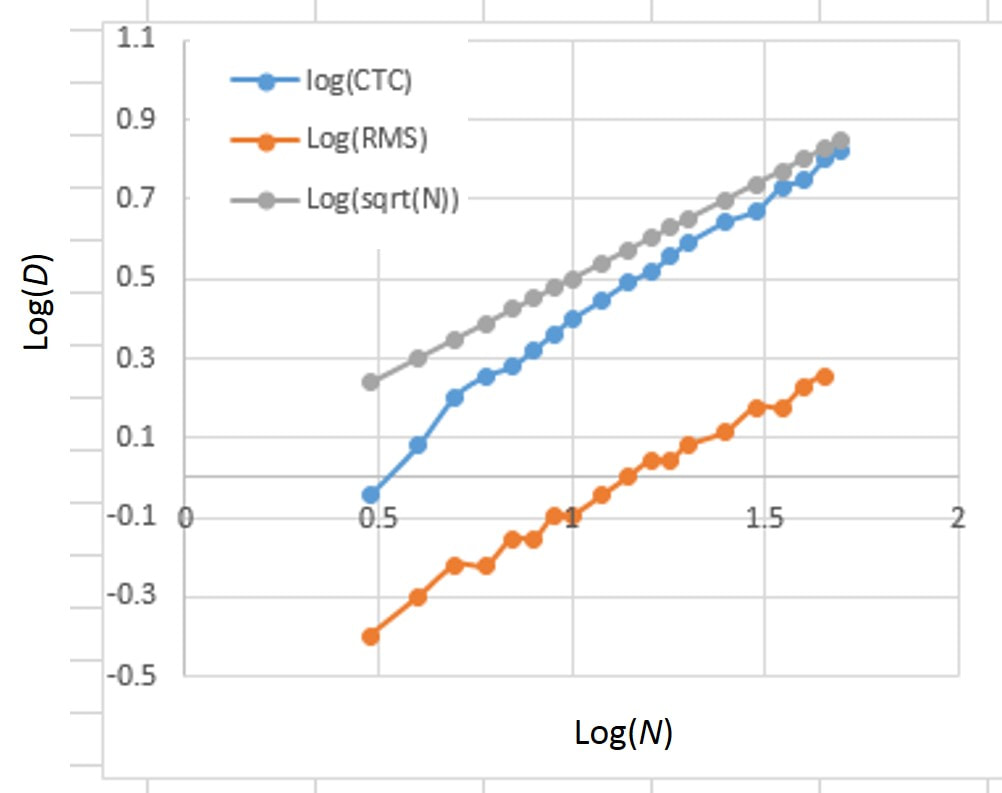
1. We can model groups shot from rifles two basic ways: either with the random walk (drunken marksman) or with the two-dice roll methods. In both cases, POI fluctuates randomly, but in the random walk we start each new shot from where the previous one hit and in the two-dice roll we always go back to the same central position and randomly jump to the next POI from there. Both methods produce groups that look like real groups shot from air rifles. The random walk group sizes scale as N^0.5 (N is the number of shots in the group), as one would expect from the basic properties of normal distributions, while the two-dice roll group sizes scale more like N^0.2 or N^0.1. The real groups shot from my LGU and FWB 124 go as like N^0.29 and N^0.36, respectively, and are somewhere in between these two scaling results. We can also expect the group size to never exceed the point of impact envelope (POIE), so we know the normal distribution scaling of N^0.5 cannot hold as N gets really big.
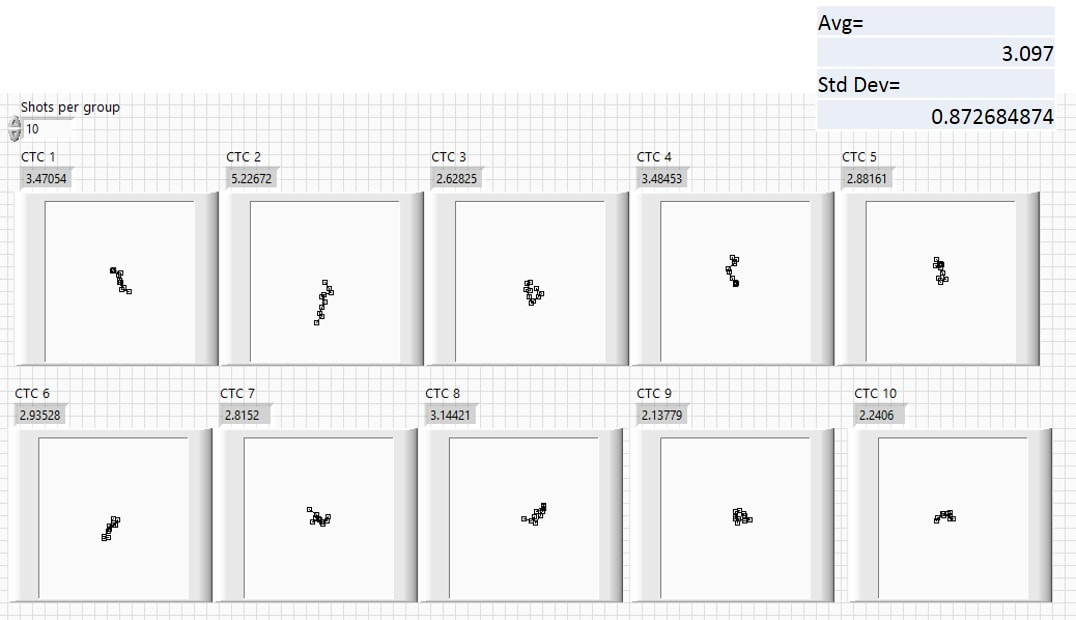
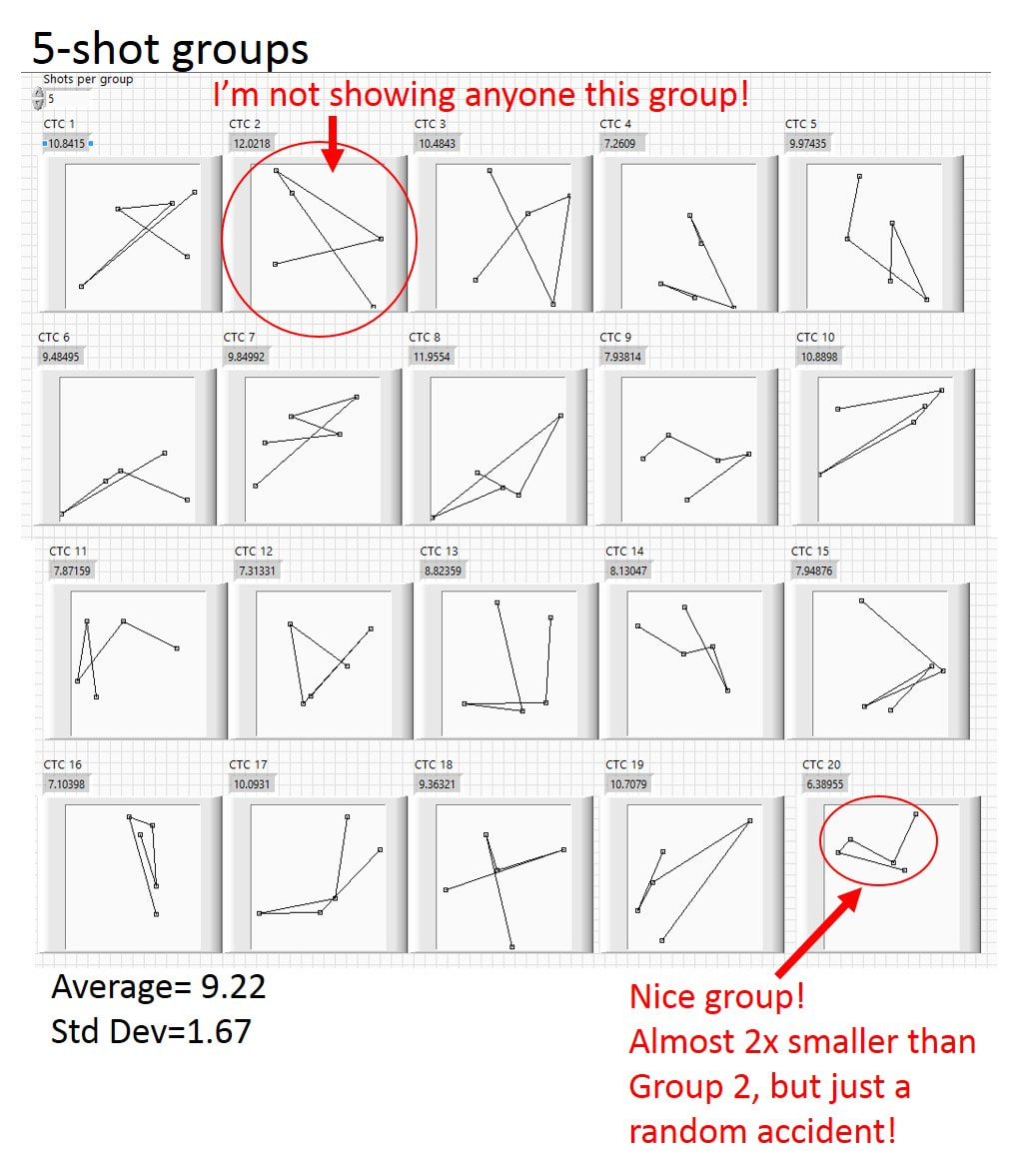
2. A single 3-, or 5-, or even 10-shot group doesn’t mean much. We can accidentally get very small groups, especially if we don’t have many shots in the group. So how many shots in a group and how many groups are needed to test the accuracy of a rifle? Part of the answer depends on how consistent your group sizes are. For example, I just shot my LGU at 10 yards and every 5-shot group was a single hole about the size of a pellet. There’s not much point shooting lots of groups with many shots in each group for that situations. At 20 yards in Chapter 2 we saw bigger fluctuations from group to group, especially when the number of shots per group was smaller, so we decided that ten 10-shot groups was more than enough. However, more data is always better. I’ve been scanning in all the targets of all my rifles for the past five years. I’ve even saved and have now scanned targets that were shot in the late 1990s. I have over 300 Powerpoint slides of targets (probably over 4000 groups!) and notes for my FWB 124 alone. Having such a digital record really helps me improve and troubleshoot these rifles.
3. After looking at the range of group sizes that we can get due to purely random fluctuations, we should not just pick the best group that we shot and use that to characterize the accuracy of a rifle. If one is shooting outdoors in the wind and one can see shots affected by the wind, then it may make sense to weigh groups more heavily where the wind was calmer than groups where one could call bad shots due to wind. This would also be true if shooting from a less stable position and one group may have been better since the shooter was able to control sway better. In those cases, the best group makes sense, but again consistency over many shots is really the key to accuracy, not just a cherry-picked group! On the other hand, in my indoor 20 yd accuracy tests, there were no external factors that could hurt accuracy. There was no wind, I used a high power scope and stable rest, and the light triggers allowed most external factors to be removed. I think any variations in the POI in Ch. 2 were purely due to fluctuations in the rifles themselves. In that case, picking the best group would really mean just picking the group where the fluctuations happened to cancel each other out a bit better. Looking at a single 5-shot group (or even worse, a single 3-shot group!) is a bit like dividing a 5 km footrace into 10 m sections. If I (a middle-aged guy who hates to exercise) ran a 5 km race against a top athlete, there could be some 10 m sections of the race where I was faster, perhaps where I sprinted like crazy before collapsing from exhaustion! On the other hand, the top athlete would post consistently short times for each 10m section of the race and would clearly beat me to the finish line. So comparing my best time for a 10m section of the race with the top athlete’s best time for a 10m section would simply not reflect reality! A single group, gives us only a very brief glimpse of a rifle’s race to accuracy. Testing and achieving high accuracy is really more like a marathon, where we look for consistency over long times and under different conditions.

 RSS Feed
RSS Feed