Probably as a result of the fantastic price that it's being offered at ($150 for a high quality gun is a great deal in anybody's book).
We have been working with the little rifle for some time now, but before we can go into "making it all it can be" we need to explain a little about how the GEOMETRY of a spring affects its characteristics.
To be quite frank, I owe a debt of gratitude to a young friend that plainly and to my face told me:
"You launched a bunch of information on materials when people do not really understand how springs even work"
So, yes, my fault. I should have posted this entry first and THEN the entry on Specialty steels now available for springs (which already have two reactions from spring/gun manufacturers). I do apologize for that and should have done things more in order.
So, Recapping:
Last entry about springs, we talked about the materials and how the different inclusions of metals as additives, or as alloying agents (not the same thing), change the behaviour of the material itself, it's capacity to store energy (as opposed to deforming permanently with it), and the spring's resistance to fatigue.
In this entry, we will explore a little about the science of "resistance of materials" and, hopefully, we will help our kind readers understand the concepts and the relationships between single characteristics/variables that make or break (pun intended) a spring in an airgun. By the end of the entry, we hope that the readers will have a fairly good understanding of what "stress" and "strain" are, what geometrical aspects of a spring define those two quantities, and how the numerical values attained by those quantities relate to the "fit for purpose" quality of the material being used for an airgun spring.
Words/Terminology
By elastic we mean that: IF subject to a force, and retained in place by some resisting mechanism (otherwise the object would simply move), THEN the material will deform in a proportional relation to the force applied.
By inelastic, we mean that the material, IF subject to a force and retained in place, will deform in a manner that is NOT proportional to the force applied.
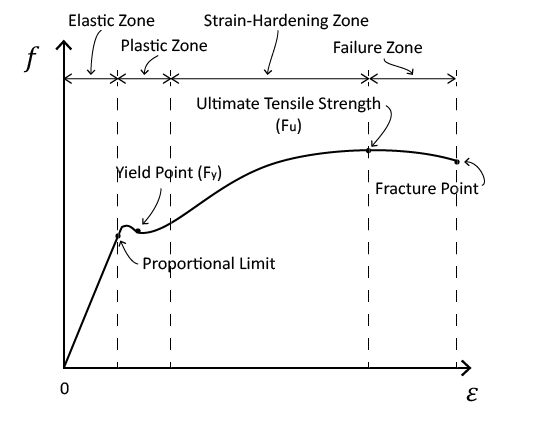
Elastic limit / Yield Limit.- We have all seen relatively stiff and hard materials (like structural steel), bent beyond any recognizable shape, whether in a car crash, an explosion, or a building collapse due to some human error (the New Orleans Hard Rock Cafe Hotel being the most recent that comes to mind), but this tells us that even a metal that is DESIGNED to be stiff and resilient, turns from elastic to inelastic when the force becomes too much to bear. Materials Science aims to understand WHY and HOW, so that materials can be improved over time.
Stress and Strain.-
Stress is what we, airgunners, understand in HPA (High Pressure Air), as "Pressure". When applied to "solids" it cannot distribute evenly all across the material, as it does in gases or liquids, but it is the same concept: A FORCE (vector) applied over a surface, its units are pressure units.
Strain is the deformation of the material when subject to a stress (note that we now do not need to establish that there is retaining mechanism because the actual presence of an INTERNAL "pressure" in the material actually tells us that the material is being restricted and is accumulating that pressure inside the material components). It does not have units, as it is a proportion of whatever dimension the material had before being stressed to the dimension of the material when subjected to said stress.
Example: Let's think of a rubber band. Simple office/household/workshop/sports device. It can be the rubber bands obtained from old inner tubes you used when you were a kid to build your slingshot, or it can be the rubber band that holds the deeds, wills, contracts, and other important documents in your house fireproof safe.
We know that, if you apply a force to extend it, while retaining the other end, the band's LENGTH grows. We may also have noticed that the band's width and thickness were REDUCED by the extension of the length.
We surely will have noticed that if you pulled too hard on your slingshot, sometimes the subsequent shots came out "weak", or that if there are too many documents in the sheaf, then the rubber band seems to not hold them as well.
It means we have exceeded the elastic limit of the rubber band. That is, the point where stress and strain stop being proportional.
Using our new words, we can say that the stress induced in the rubber band by our pulling exceeded the allowable strain (yield point) for the rubber used in the band.
Savy slingshot builders will know from experience that there are many ways to build a better slingshot, but probably the easiest is to use surgical tubing instead of rubber bands made of cut inner tubes.
By improving on the material used, we built a better product.
Interesting so far, but, if you stop to think: ¿Can you compress a rubber band?
Hmmmm.- not really so, ¿how come we can compress steel springs, but not rubber bands?
Of course the answer lies in the geometry, but also in the way the molecules/atoms of materials stick to each other.
Some materials form crystals, some create amorphous structures. A Crystal is just a material where the molecules of the material are arranged in a geometric pattern, and therefore they resist pretty well any force that tries to tear them apart (operative word here is TEAR).
An amorphous material is a material where there is no geometric pattern, but still the molecules bind to each other by electromagnetic forces and therefore resist forces in a less "stiff' way, but they do resist deformations.
That sounds logical? Hope so, it still does not answer why we can compress steel springs, but not rubber bands.
Are there any examples of pure crystalline materials? Almost. Jewels are a good example, they are not perfect because even the most perfect diamond will have inclusions and flaws. It is THESE that the experienced cutter uses to split a large chunk into smaller pieces that can then be sold as the engagement ring stones that start most couples in the long road to family bliss.
IF the rough diamonds were perfect, there would be no way of cutting one in an orderly fashion and the huge gem would most likely explode if someone tried to cut it. It would have to be eroded/ground away little by little and a huge "rock" would be the result, like the British Crown Jewels.
Is there a perfectly amorphous material? Play Doh comes to mind. It does have SOME spring to it, but very little, so that little hands can create things out of it.
Between these two extremes, everything else in the world finds a place.
Now, ¿why steel?
We use steel because it is a fairly abundant mineral (Iron/Fe), therefore cheap. And we have been doing research and development on it for about 3,200 years.
HEY! Someone will say: We still do not know why we can compress steel springs and not rubber bands!
Yes, I know, we're getting to that, Patience and Perseverance, my young Padawan.
So, Iron, in its relatively wild state, is an amorphous material (Iron Oxide for the most part). and even when reduced in a kiln and rendered into ingots, the amount of carbon inclusions present as a result of the smelting process will make the "pig iron" fairly brittle. ¿Is it brittle because it is crystalline, or because there are lots of impurities and inclusions? Actually both.
PURE iron would be a crystal (actually there are two types of iron crystals, both cubes), albeit unstable ones (but that would be getting into Quantum Physics and that is beyond the scope of this entry), and so it would be brittle. It is also brittle because the casting process creates stresses along lines of non-homogeneity (impurities and inclusions), and because SOME forms of steel in the iron would actually act like a "wedge" in the material and make the stress fractures grow rapidly and uncontrollably.
Assuming a very high degree of purity in the iron, then it would bend easily. Not much stronger, stiffer, nor resilient than the best Bronzes.
So, we refine and change the pig iron into steel by including and diffusing the carbon content (reduction process of the oxide, and then purposely oxidizing the excess carbon by blowing air into the molten metal), and then increase the content of other metals, and non-metals, to increase other characteristics (hardness; stiffness; resistance to fatigue, to high or low temperatures, to oxidation, etc); from Molybdenum and Vanadium, to Copper, Silicon, Manganese, Chromium, Nickel, and Cobalt.
Now, the elements above mentioned, whether added as alloying agents, or as additives, diffuse themselves into the crystalline lattices that iron forms. And when temperature is changed dramatically (quickly) either in a quenching, tempering, drawing or other thermal process, then further compounds form: Carbides and Silicates being the prevalent ones. More important than the compounds is how the crystalline structure in the steel changes with heat treatments.
When we said that Iron creates two types of crystals, we were referring to a Body-Centered Cube (2 Iron atoms) that is called Ferrite, and Face-Centered Cube (4 Iron atoms), called Austenite.
When the Austenite cools down abruptly, it shears the cubes into two tetrahedrons, where the carbon is diffused into a much more compact space, and therefore the crystal itself exhibits very high "strength". Problem is that it also become brittle. These tetrahedrons structures are called Martensites and they are the ones most responsible for the hardness in steel.
Since the crystalline structure change is forced by thermal processes, it is mostly, and controllably, reversible. So, for every quenching, there must be a tempering and a drawing, in order to create a material that is "balanced" between hardness, stiffness and resistance to breakage.
Now that we have explained how the physical properties of steel change due to the change in the crystalline structures, we can say it:
We CANNOT destroy any material by "pure compression" . We can compress materials but compression by itself does not induce neither stress nor strain.
If you remember, when we stretched the rubber band, we observed the thickness and the width of the band to decrease. THIS is what WE call "compression", but in reality is the RESULT of a stretching.
The PROPORTION between the elongation in the direction of the stress that is being applied and the contraction in the perpendicular direction is the Poisson Ratio for that material.
In the same fashion, if we were to have a perfect cube of steel that we put it in a press and then apply force on it, it will fail not because we are compressing the material, but because the material that we are compressing is placing a STRETCHING force sideways into the surrounding, unsupported, material, and that is what tears the material apart (¿remember I told you that the operative word was TEAR?).
If I am not making too much sense, consider the same case, but in a hydraulic environment, where we apply a force to the fluid, and the fluid itself applies evenly and in all directions, a pressure to the steel cube.
¿Do you think it will fail?
.
.
.
Nope!
Let's conduct a "thought experiment":
Think of a material as a collection of "leaves", formally called lattices, and then let's think about how important is the directional connection of the internal structures of the material.
Imagine a sheaf of paper. While it is packed and in the wrapper, it can be incredibly strong and behave almost a like a solid brick. You can stand it upright and you can stack a bunch of them one on top of the other.
BUT, if we remove the wrapper and try to stand a single one on its own, it will collapse.
While on the wrapper, we cannot bend a whole ream, but out of the wrapper, the whole ream can be bent and fanned, and "aired", as we used to do with the feedstock of old copying machines.
IF we apply enough force to a wrapped ream of paper, it will BREAK the wrapper, if we apply a little force, and then place it on a table it will return to is prismatic shape out of its own weight.
In one case we have exceeded the yield strength of the material, in the other we have not.
Important here is to stress that, when out of the wrapper, if we bend the ream one way, there will be one end that becomes "longer", if we bend it the other way, then it's the other end the one that becomes "longer".
In the middle, there will be one sheet that keeps its apparent length, and we will call that the "Neutral Fiber"
So, back to steel airgun springs: ¿What on earth are we doing when we compress the spring?
Savy airgunners and specially those tinkerers that turn their own spring guides know that springs will increase in Outside Diameter (D) when compressed.
If you think about it, a length of metal can only increase its length if it is being STRETCHED. So, when we compress a steel spring, in reality we are stretching each and every coil.
This stretching is what induces the stress and the strain, and it is the reason why we must pay special attention to the SURFACE of the spring. Any imperfection or point of stress concentration will start a micro-fracture that, in the end, will break the spring.
Reason why good quality springs are shot peened and / or covered with some material that prevents the formation of micro-cracks.
Usually, when we receive a spring from a manufacturer, it is longer than expected, unless we specify that we want our springs to be shipped "set". In this case, the spring manufacturer will compress the spring to solid and then ship it to us. By compressing to solid, the yield / elastic limit is reached and the spring is reduced to the shortest possible length. No further compression cycles can exceed the yield limit of the new conditions (length and diameter), and therefore all further usage will happen within the elastic limit of the material in question.
Can we make springs out of other materials? Yes, and we do. Beryllium bronze is used in explosion proof applications, copper is used in some other -mainly electrical- applications, even aluminum can be used but it's very limited; hopefully, once we master the creation of crystalline aluminum ("Transparent Aluminum" of Start-Trek fame), we will have a fantastic material, specially for scope building. That, though, is several years into the future.
One last thought experiment: If you drop a steel ball bearing into an anvil, it will re-bound. But, it will not rebound to the same height it was dropped from. Even in vacuum.
And if we measured the temperature of the steel ball, we would see that after many re-bounds the temperature has gone up slightly. ¿What is happening?
What is happening is that even the hardest of steels that can absorb huge forces and not yield, still cannot return 100% of the received energy.
SOME energy is lost in the INTERNAL FRICTION of lattices and molecules that bend and suffer recoverable internal displacements.
The SUM of all these INTERNAL energy losses is called Hysteresis
Now, putting it all together:
A material can receive a stress, accumulate it as a strain, AND RETURN IT as a force, only when the elastic yield limit has not been reached.
It will not return ALL the energy, some portion of it is inevitably lost to hysteresis.
The Elastic Yield Limit will be determined by the structure of the material as much as by the chemical and crystalline arrangement that is controlled by post material manufacture heat treatments.
So, now that we understand how springs work; how materials work, and fail; and how we need to look at the limits of the material to select a "fit for purpose" material for our springs, we can go into the GEOMETRY.
Equation
And yet, this equation says nothing more scientific than if I would assert: "The moon is a huge, spherical, rock that goes around the earth in ever increasing ellipses governed by Newtonian physics"
Both, the equation and my assessment, are true and consistent with the human experience of thousands of years. Both give humans a good frame of reference to study the object of interest, whether it is the moon, or the coil spring. Both can yield good insights into what the effects of changes can be.
And yet there is a degree of empiricism into both, they are not "pure science".
The reason is simple: since the formation of the moon from the proto-earth to the present, there have been many phenomena that have taken place that we can neither prove, nor disprove. So we can only establish theories of HOW the moon came to be, WHY it is going away, and WHAT happened in the past that cannot happen in the future because the distance to the moon is only increasing.
In the same way, the complication of a coiled wire that changes apparent cross-section with each millimeter of compression, that is subject to microscopic heterogeneity and that can have vastly different characteristics, while at the same time having vastly different histories, is very hard to pin-point.
BUT
The experience of the last 162 years (since the machine to economically make coil springs was invented), has shown that it is "Close enough".
And, so, let's take element by element in the equation into analysis and consideration:
"k"
k is the constant of the spring. In other words, how much force it can store for a given length of compression. You can think of it as lbs(force)/in, or Newtons/m, or kgs/m, or oz/in, or . . .
In the end, you will have a rifle with a power stroke of length "X" and you will want a spring that can develop "Y" force, so that the piston can be accelerated and pushed into the compression chamber that will make the air inside go through the transfer port and push in its turn the pellet out of the barrel, ¿no?
So, given an ARCHITECTURE of a gun (power stroke, bore, swept volume, piston's mass, and transfer port length) we can estimate how much force we will need, and therefore, what characteristics of the spring we need to achieve.
OR, assuming an average efficiency of the basic airgun architecture, we can also start from desired energy yield at the muzzle and go back all the way to the force required and therefore the "k" we need to achieve within the constraints of both the gun and the spring material.
So, let's simplify, clarify, and amplify (SC&A):
"k" just means how strong the spring will be, given a length of compression, it comes from Hooke's Law that states that 'F=kX' where F stands in for Force, k is itself, and X is the power stroke.
"G"
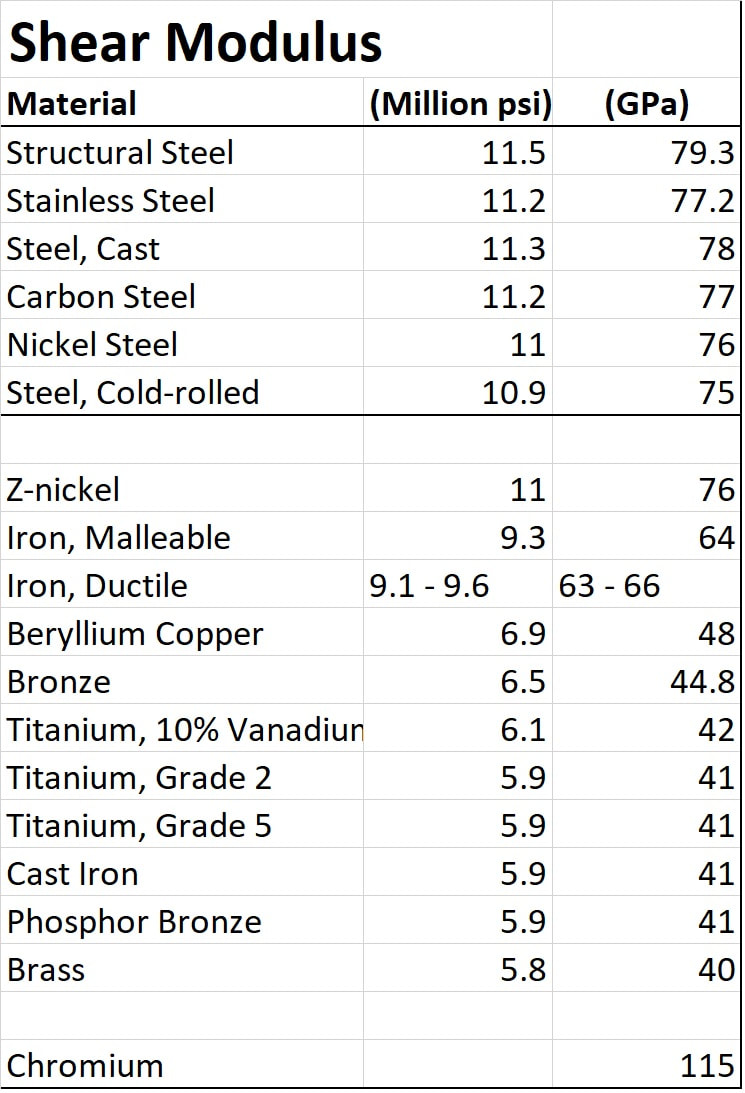
Is the "Shear Modulus". It means how rigid a material is, how much stress is required to create the necessary amount of strain that will tear the material apart.
It CAN be calculated using the Elasticity/Young's Modulus (the tangent of the angle of the line that describes the stress-strain behaviour of a material in the linear -elastic- zone; also called the slope of the curve in this first section -before the yield point-) and the Poisson Ratio (the relation between a stress applied in a direction with the strain created in a perpendicular direction).
I am including other materials just for the sake of comparison, and if we go to serious spring makers' websites, some of them list the characteristics of the materials they use.
Still, a pretty much uniform value for G is around 79.3 GPa for ALL steels that are of viable use, whether they are labelled as "valve" or "specialty" steels.
So, SC&A: G is, for all intents and purposes, an empirically derived value that for airgun use should be taken as the constant 79.3 GPa/11.5 Million PSI
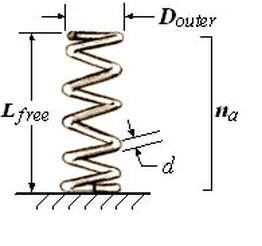
"d", "D", and "na".-
"d" Is the diameter of the wire used. Using a fairly standard diagram:
A little like calculating a center to center group size: You measure the two farthest edges of the two extreme shots and deduct a caliber. Same process, same principle, same arithmetic.
"na" is the number of active coils, which for most purposes (except Vortex's PG-3), would mean the number of coils that are ACTIVE, therefore the two end coils do NOT count.
As usual, since the advent of computers and the internet, there are online calculators that do the number crunching, this is one of them:
https://www.acxesspring.com/spring-calculator.html
and it is fairly easy to use.
Let's try an example:
We take the 640 T spring from ARH's website:
https://www.airrifleheadquarters.com/catalog/item/251488/8128905.htm
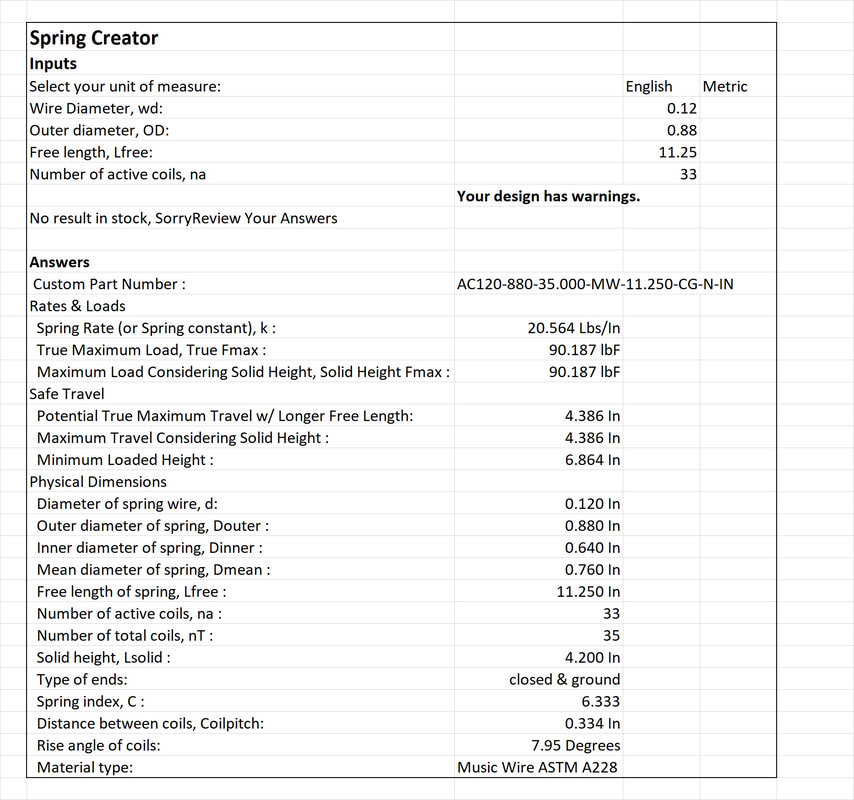
Just because it is new and it provides an interesting contrast with most other springs offered. It is a WIDE spring : 0.640" ID, with a relatively thin wire: 0.120", 35 coils and an OAL of 13.25" (unset).
The 0.640" ID would mean a 0.880" OD and a "D" of 0.760" or 19.3 mm's
So, what would the calculator predict?
But, what would happen if we increase the Wire diameter (for the purpose of this numerical simulation, we will change ONE thing at a time.
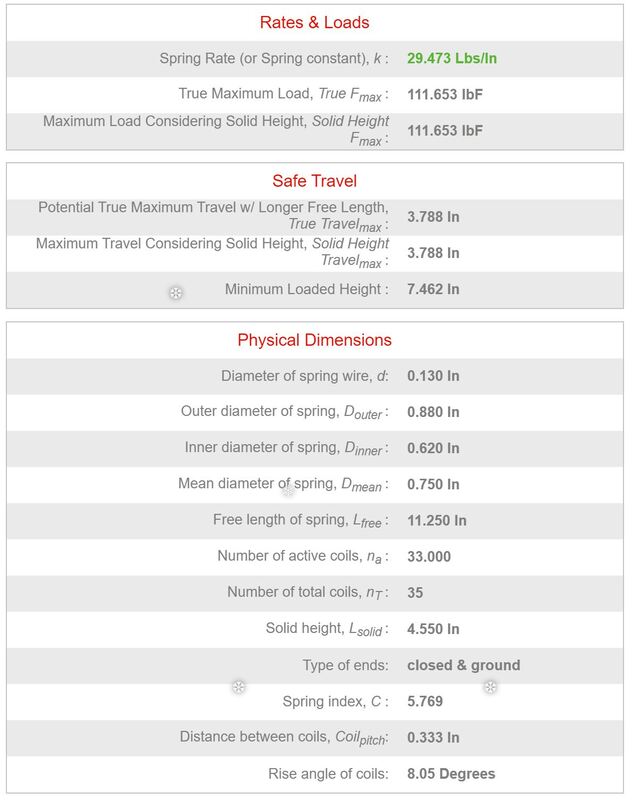
Let's go to 0.130" wire:
But then, remember the equation? In the equation, the d is raised to the 4th power, so a 9% increase in wire diameter would imply over 40% increase in k.
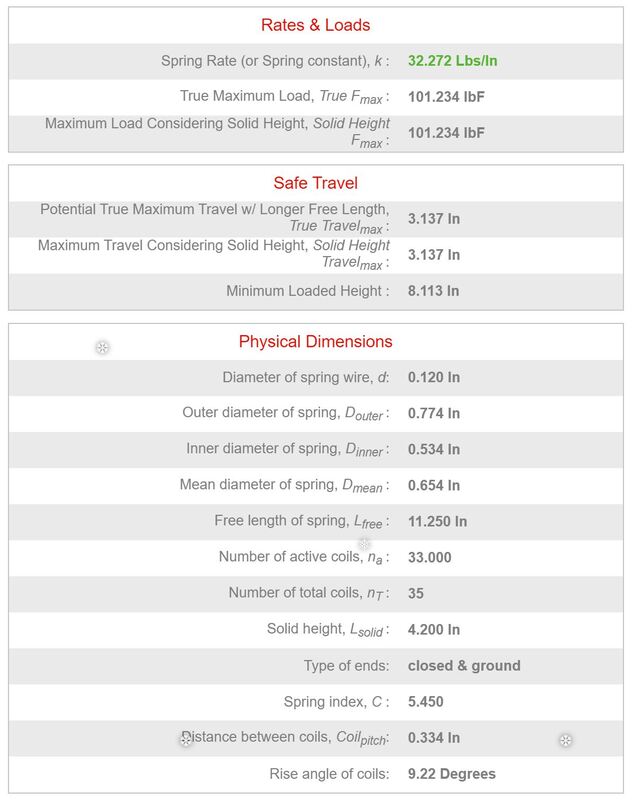
What would happen if we had REDUCED the mean diameter of the spring?
Let's go back to our 0.120" wire and reduce the OD to 0.774" that would imply a D of 0.654:
Why that value? because that value gives an ID of 0.534" that is a tight fit into the OEM DIANA spring guides.
What would the equation have predicted?
A reduction of 14% gets raised to the power of 3 in the divisor, so the net effect is an increase of 57%
For a base case of 20.564, a raise of 57% would mean 32.27 #/in, so we now have a feel of how changing one aspect affect the outcome.
The last variable we can play with is the number of active coils, but that is an inverse relation, so it is not too complicated to imagine what effect reducing, or increasing the number of active coils will have in the result.
Conclusions
We can increase the d, within limits, and every gun will achieve a "plateau" where more force will not increase muzzle energy because the swept volume has been completely used.
The biggest possible OD will yield the least stress in the spring, therefore, this will guarantee the longest and most stable life possible.
For most calculations, the springs we use in airguns are doomed to failure because calculations cannot take into account the effect of a guided spring (fore and aft). SOME calculators do, but you need to pay for them and it is not in the intent of this blog to make you pay for information.
Most spring makers would balk at the duty cycle we submit our springs to. But then they are concerned mostly with industrial applications where millions of operations are desired before you need to shut down the plant for maintenance. Maintenance, for some of us, is part of the hobby.
In the next blog entry, we will deal with what can be done to the DIANA 430L, short of changing the cocking lever arrangement, because that will be looked into in another blog entry that will deal with efficiency of powerplants.
Hope you have enjoyed this trip into the rarefied world of the airgun designer.
I apologize for the length of the entry and thank you all for staying with the thread of ideas. It is a complicated aspect to explain and I hope I have not confused everyone even more.
;-)
Keep well, shoot straight, and if I don't get the time to write the entry for the 430L before the holidays come tumbling down on us, like the walls of Jericho, I wish you all, the best of peaceful, contented, filled with family and friends, holidays!
HM
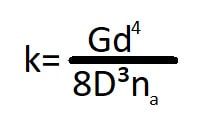
 RSS Feed
RSS Feed